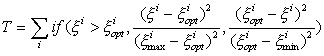Назад, на численное моделирование

Модуль генерации сетки (вначале разбиения плоской области на треугольники, потом поверхности на треугольники и затем разбиение пространственной фигуры на тетраэдры) разрабатывался во времена, когда в Интернете алгоритмы найти было практически невозможно, искать и перелопачивать гору периодики возможности не было, проще самому было сделать, чем искать и изучать алгоритмы, разработанные ранее...

1. Фронтальные алгоритмы построения треугольной сетки.

Исходными данными для фронтальных алгоритмов является граница расчетной области, представленная в виде отрезков (сегментов). Начиная с минимального радиуса кривизны границы области, происходит последовательное создание новых треугольников (рисунок 1.1), с продвижением границы в глубь триангулируемой области.

Фронтальные алгоритмы являются более устойчивыми к нерегулярности отрезков на границе и позволяют разбить на треугольники произвольную область, в том числе многосвязную (например, область с «дырками», см. рисунок 1.1).

Выбор метода построения сетки зависит от требований, предъявляемых конкретной задачей к сетке и самому методу триангуляции. Мой выбор пал на фронтальные алгоритмы потому, что они наиболее полно удовлетворяют требованиям, предъявляемыми задачами, с которыми я имею дело (для произвольных областей на плоских и трехмерных поверхностях, с определенной степенью неравномерности сегментов на границе, автоматически получать на выходе сетку с максимальной равномерностью треугольников). Началось все с необходимости автоматически перестраивать сетку при образовании трещины в 2 D расчетах, после этого была сделана автоматическая генерация начальной сетки в плоскости и на произвольной поверхности.

Задачи в разных областях знаний предъявляют разные требования к равномерности генерируемой сетки, где-то требуется равномерность (или ограничение) по площади треугольника, где-то по максимальной/минимальной стороне, где-то по минимальному углу и т.д. Поэтому, в любом методе вводится критерий равномерности достраиваемых треугольников, который, в частности, для фронтальных алгоритмов должен обеспечивать устойчивость процедуры триангуляции, т.е. степень неравномерности новых элементов должна уменьшаться по мере уменьшения неразбитой области. Другими словами, при наличии нерегулярных сегментов на границе, процедура должна обеспечивать выход на «равномерный» режим по мере сужения области.

Для конечно-элементных методов под равномерностью понимается приближение треугольника к равностороннему с длиной стороны, равной заданному значению ∆х. В общем случае сетка может иметь сгущения (например, на концентраторах напряжений), при этом ∆х умножается на некоторую весовую функцию ∆х=∆х* p( x, y, z) (в области сгущения p( x, y, z)<1). Под устойчивостью мы будем понимать уменьшение «нерегулярности» новых треугольников по мере уменьшения недостроенной области.

Введем понятие функции отклонения – количественную оценку отклонения от равномерности. Будем считать приемлемым, если каждый треугольник удовлетворяет следующим условиям:

• Разброс граней в диапазоне [0,8..1,2]∆x (1.1)
• Разброс узлов в диапазоне [40..90] градусов

Функция отклонения должна учитывать оба этих условия. Остальные величины (площадь, высоты и т.д.) можно отнести к вспомогательным параметрам. Для равностороннего треугольника со сторонами, равными ∆x, функция отклонения должна быть равна нулю, в диапазоне допустимых значений ее изменение должно быть слабым, вне допустимого диапазона – более резким. Этим требованиям удовлетворяет простая параболическая зависимость, нормированная к границам допустимого диапазона:

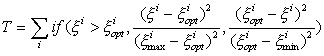(1. 2)

где суммирование выполняется по всем критичным параметрам. Для треугольника с гранями x1, x2, x3 и углами α1, α2, α3, при использовании требования (1.1), функцию отклонения можно записать в виде

(1.3)

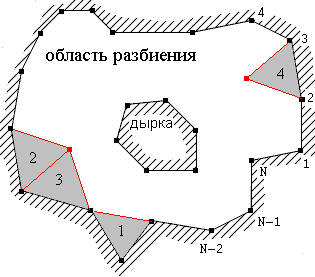
Рисунок 1.1 Триангулируемая область.

Представим границу в виде замкнутого списка из N элементов, в котором каждый элемент (узел) знает предшествующий ему узел и следующий за ним, причем за N-ым узлом идет 1-ый. Область, которую требуется разбить на ячейки (рисунок 1.1), находится слева при обходе границы. Слева или справа в данном случае не играет особой роли, главное – четко знать, по какую сторону от отрезка находится область триангуляции. При наличии «дырок» (многосвязная область) это тоже следует учитывать.

Фронтальный алгоритм заключается в том, что на границе области последовательно создаются новые треугольники, за счет этого недостроенная область постепенно сужается, а граница (список узлов) корректируется на каждом акте создания треугольника. Вариантов достроения новых треугольников всегда достаточно много, как с точки зрения места на границе, так и с точки зрения способа (см. рисунок 1.1):

- «Одиночный узел» - достраиваем новую ячейку (треугольник № 1). Вариант оптимален для узлов с острыми углами.

- «Двойной узел» - создается новый узел, достраиваются две ячейки (треугольники № 2 и 3). Вариант оптимален для узлов с тупыми углами (близкими к 120°).

- «Свободный вынос» - создается новый узел, достраивается ячейка (треугольник № 4). Вариант оптимален для узлов с углами, близкими к 180° или больше.

Собственно, выбор наиболее оптимального варианта на каждом шаге и есть основная тонкость фронтальных алгоритмов, здесь следует помнить, что задача заключается не в том, чтобы на каждом шаге создавать максимально равномерный треугольник, а в том, чтобы по окончании процедуры степень нерегулярности самых «кривых» треугольников была минимальна.

Я использую следующую последовательность действий:

Шаг 1. Для всех узлов на границе недостроенной области, выпуклых наружу и имеющих угол<150°, определяется, какой вариант достроения, «одиночный» или «двойной» более подходит для данного узла. Для углов, меньше 40°, такая проверка не производится, он и так слишком острый, чтобы разбивать его на две части (в случае, если область "правильная", выпуклая, а длина отрезков на границе имеет малый разброс, значение минимального угла можно повысить до 60°).

Оптимальным считается вариант («одиночный» или «двойной»), для которого минимальна штрафная функция, которая вычисляется следующим образом. Для «одиночного» варианта вычисляется функция отклонения (1.3) по 3-м углам и 3-м граням. В случае, если угол β1 (рисунок 1.2) между лучом U_k-1U_k-2 и новой гранью U_k-1U_k+1 меньше 40°, определяется функция отклонения и для треугольника U_k-1U_k-2U_k+1. Аналогично для угла β2 между лучем U_k+1U_k+2 и новой гранью (рисунок 1.2, заштриховано голубым цветом). Итоговым значением штрафной функции для «одиночного» варианта считается максимальное значение функции отклонения из этого набора:

S1=Max{ T(U_k-1U_kU_k+1) [,T(U_k-1U_k-2U_k+1)] [,T(U_k-1U_k+2U_k+1)] }

Для «двойного» варианта штрафная функция тоже берется как максимальное значение аналогичного набора функций отклонения: для каждого из новых треугольников, а если углы βi между новыми гранями и лучами U_k-1U_k-2 (U_k+1U_k+2) меньше 40°, то и для соответствующих треугольников (рисунок 1.3, заштриховано голубым цветом):

S2=Max{ T(U_k-1U_k ), T(U_k+1U_k ) [,T(U_k-1U_k-2 )] [,T(U_k+1U_k+2 )] }

Если в итоге S1< S2 (штрафная функция будет минимальна для «одиночного» варианта ), в узле устанавливается соответствующий признак. Шаг №1 нужен, для того, чтобы в ситуациях, когда угол в узле близок к 90°, определить, какой вариант достроения предпочтительней, так как критерий «угол<90° - один треугольник, угол>90° - два треугольника» не обладает устойчивостью (он не учитывает длину сторон и не учитывает ближайшее окружение).

Шаг 2. Из множества узлов с «одиночными треугольниками», выбирается тот, у которого Min(β1,β2) максимален. Требование достраивать «одиночные» узлы в определенном порядке продиктовано условием устойчивости. Варианты сортировки рассматривались и другие - по минимальному углу (рисунок 1.4), по минимальной новой грани (рисунок 1.5), по минимальной площади (рисунок 1.6); собственно, на рисунках видно, что в некоторых случаях их применение приводит к неудовлетворительным результатам. В то же время критерий по максимальным углам β обеспечивает устойчивость даже в ситуациях, когда длина отрезков на границе различается более, чем в несколько раз (рисунок 1.7). На мой взгляд, даже сортировка по минимальной штрафной функции S1обладает меньшей устойчивостью.

Здесь стоит отметить, что возможна ситуация, когда угол βi≤0 (рисунок 1.5). Эти варианты даже рассматривать не стоит, так как они некорректны – возникает «перехлест» сетки и образуются ячейки с отрицательной площадью.

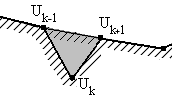
Рисунок 1.8. Достроение «одиночного» узла.

Если «одиночные» узлы есть и один из них нас устроил, создаем ячейку, граница корректируется (рисунок 1.8, узел U_k удаляется из списка). Возвращаемся на шаг № 1.

Шаг 3. В случае, если подходящих «одиночных» узлов нет, пытаемся достроить «двойные» узлы. При наличии подходящих (выпуклых наружу, с углами меньше 150°), создаем новый узел , достраиваем две ячейки, граница корректируется (рисунок 1.9, узел U_k в списке заменяется новым узлом ). Возвращаемся на шаг № 1.

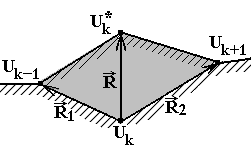
Рисунок 1.9. Достроение «двойного» узла.

Координаты узла определяются (еще на первом шаге) из условия минимума функции отклонения по 3-м новым граням и 6-ти углам. Начальное значение берется как , где:

;

квадратные скобки обозначают операцию нормирования, означает 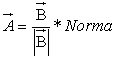, т.е. - вектор, параллельный и имеющий длину, равную Norma.

Если на шаге 3 точка оказывается слишком близко (рисунок 1.10,а) от узла U_k+2 (или U_k-2), то узел определяется как точка пересечения биссектрис (рисунок 1.10,б) из углов U_k и U_k+1 (или U_k и U_k-1).

Шаг 4. Если все U_k>150°, то берем вектор (рисунок 1.11) в виде 1[∆x] и поворачиваем его на 60° против часовой стрелки.

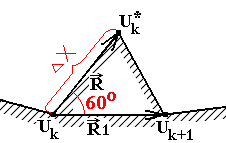
Рисунок 1.11. «Свободный вынос».

Если созданию узла ничего не мешает, определяем ячейку и включаем узел в список между узлами U_k и U_k+1. Если учитывать ближайшее окружение, то треугольник можно создавать не равнобедренным (для выпуклых углов поворачивать на 1/3 угла, а не на 60°). Еще стоит отметить, что на данном этапе надо следить за тем, чтобы углы U_k и U_k+1 были больше 150° (если они по тем или иным причинам не подошли для достроения по типу «одиночный» или «двойной узел», «свободный вынос» для них тем более не подойдет).

Данная последовательность действий продолжается до тех пор, пока число узлов в списке не станет равно N=4. Если расстояние от центра 4х-угольника (среднее от координат узлов) до каждого узла ≥0,7∆x, то в центре создается узел и четырехугольник делится на 4 ячейки, иначе создаются 2 ячейки (диагональ проводится из тупейшего узла).

Если область триангуляции многосвязная, то есть ее граница представлена в виде нескольких непересекающихся линий, то на каждую линию связности вводится свой замкнутый список и заполнение области происходит согласно описанному выше алгоритму, пока новая точка не окажется слишком близко от другой линии связности. В данной ситуации списки объединяются и число линий связности уменьшается на единицу.

Все, что здесь описано, не есть описание какого-то конкретного метода, это «метод решения», который использую я (его эволюцию можно проследить, сравнив с тем, что описано в диссертации). Варианты функций отклонения не мешало бы по- оптимизировать… Вполне возможно, есть алгоритмы, работающие быстрее и создающие более равномерную сетку… Создание сеток – это отдельная задача, но для меня это лишь инструмент и специализироваться на ней я не могу.

2. Определение окружения при создании нового узла

При создании нового узла, необходимо убедиться в том, что он будет расположен на достаточном расстоянии от уже существующих узлов и отрезков. Для этого необходима специальная процедура, которая
- определяет тип близости
- определяет список узлов, располагающихся в опасной близости от новой точки.

Тип близости необходимо определять для того, чтобы принять решение о том, отказываемся ли мы от создания узла, корректируем ли мы его координаты, или ему ничего не мешает. Определяется критическое расстояние Rкр=min(∆x, R0), где R0-расстояние до узла U_k, от которого осуществляется вынос точки. Для всех узлов (за исключением U_k, U_k-1, U_k+1 – они не могут мешать, так как при определении координат новой точки учитывается их положение) проверяется расстояние до новой точки. Если для хотя бы одного узла на «родной» линии связности (на которой расположен U_k) расстояние < 0,7Rкр, отказываемся от создания новой точки, кроме ситуации, изображенной на рисунке 1.10, где координаты нового узла корректируются.

Если узлы на «родной» линии связности не мешают, необходимо проверить узлы на других линиях связности. В этом случае критическое расстояние надо брать больше, чтобы не упустить момент для корректного создания перемычки между линиями связности. Если какой-то узел окажется слишком близко, создается «мостик» между линиями связности и они объединяются. Если расстояние между узлом U_k, от которого осуществляется вынос точки, и противолежащей границей <1,2∆x, узел U_k соединяется с ближайшей точкой на противоположной границе, чтобы в итоге получить замкнутый список, охватывающий узлы на обоих линиях. Здесь есть некоторые тонкости, узлы на «мостике» будут в списке дважды, так как при обходе границы (по правилу «неразбитая область слева») «мостик» пересекается дважды. Если же расстояние больше, чем 1,2∆x, то новая точка все-таки создается (с учетом расстояния до всех ближайших узлов) и «мостик» строится уже от нее.

3.Post-оптимизация сетки

Обеспечить максимальную равномерность сетки, используя фронтальные алгоритмы, практически невозможно – это потребовало бы учитывать при достроении каждого треугольника абсолютно все его окружение, как в достроенной области, так и в недостроенной, что противоречит принципам фронтального алгоритма. Однако к произвольной сетке можно применить (по крайней мере, при подготовке конфигурации для расчета) post-оптимизацию, которая позволяет значительно улучшить равномерность сетки и выправить определенные нерегулярности. Критерий равномерности при этом может быть иным, чем при начальной триангуляции.

Post-оптимизация включает в себя смену диагоналей в виртуальном четырехугольнике, образованном двумя треугольниками (рис. 3.1) и изменение координат внутренних точек в области. При смене диагоналей используются одновременно два критерия:

Критерий по числу ячеек в узле. Максимально равномерная сетка соответствует равносторонним треугольникам, соединенным по 6 штук в каждом узле. Для узлов на границе оптимальное число ячеек берется как внутренний угол, деленный на 60 градусов (полученное значение округляется). Для узлов Uk (рис. 3.1), в которых меньше 6 ячеек, критерием смены диагонали в ячейке ABD является условие

(3.1), где:

n*– оптимальное значение числа треугольников для соответствующего узла;
n – текущее число треугольников в соответствующем узле;
m – число треугольников в соответствующем узле, при условии смены диагонали;

То есть критерием является уменьшение суммарной погрешности (отклонения). Если у узла Uk будет несколько ячеек, для которых выполняется условие (3.1), то выбирается ячейка, у которой уменьшение погрешности будет максимальным.

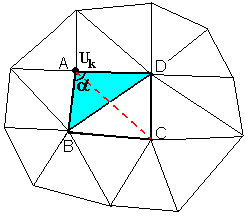
Рисунок 3.1. A: n=4; B: n=7; C: n=5; D: n=8.

Критерий тупого угла. Для каждого тупого угла α (рис. 3.1), диагональ, как и в первом критерии, меняется, если выполняется условие 3.1 (суммарная погрешность уменьшается).

На первый взгляд, описанные критерии смены диагонали могут показаться эквивалентными, однако, это не так. Например, для узлов на границе невозможно применить первый, а второй зависит от начальной равномерности сетки.

При изменении координат внутренних точек применяется итерационная процедура: для каждого узла находится такое положение, при котором сумма (по всем ячейкам узла) функции отклонения достигает минимума. Вид функции отклонения зависит от того, для каких целей мы оптимизируем сетку, и может включать в себя произвольную комбинацию отклонений углов, длин граней и площади ячейки от соответствующих оптимальных значений (возможно, с учетом весовой функции p( x, y, z), позволяющей сгущать сетку в определенных областях). Я в качестве функции отклонения, для Post-оптимизации, использую сумму отклонений площади и всех трех углов от их оптимальных значений - углы обеспечивают приближение к равносторонним ячейкам, а площадь обеспечивает равномерный размер. Если все узлы в области содержат по 6 ячеек, то эта процедура дает превосходные результаты. К сожалению, это не всегда возможно, так как граница вносит определенные возмущения и при триангуляции поверхности в трехмерном случае, при значительном радиусе кривизны, присутствуют узлы с иным числом ячеек. Собственно, смена диагоналей как раз и призвана подготовить почву для вызова данной процедуры.

Последовательность применения различных алгоритмов – нетривиальная задача. Как правило, я использую следующий порядок:
1 шаг) Смена диагоналей по критерию числа ячеек в узле;
2 шаг) Итерационное изменение координат внутренних точек;
3 шаг) Смена диагоналей по критерию тупого угла;
4 шаг) Итерационное изменение координат внутренних точек;

Результат триангуляции области, заданной окружностью, представлен на рисунках 3.2-3.3:

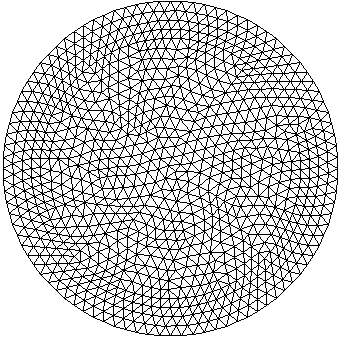Рисунок 3.2. До процедуры Post-оптимизации

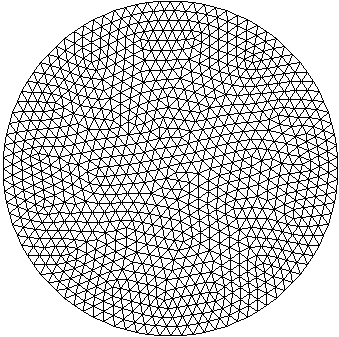Рисунок 3.3. После процедуры Post-оптимизации

4.Триангуляция криволинейных поверхностей

При триангуляции области на криволинейной поверхности, заданной уравнением f ( x , y , z )=0, все вышесказанное остается справедливым, лишь уточняются следующие моменты:

I ) Первоначальная граница (точнее, точки, ее задающие) должна лежать на поверхности, то есть удовлетворять уравнению f ( x , y , z )=0. Если требуется разбить сетку на сложной поверхности, на разных участках описываемой разными уравнениями, то удобно разбивать последовательно области, границы которых являются пересечением поверхностей. Например, для триангуляции поверхности цилиндра выделяем нижний торец, верхний торец и боковую поверхность – в каждой их областей уравнение поверхности f ( x , y , z )=0 не меняется, на границе нормаль определена (по отдельности для каждой области, а больше нам и не нужно).

II ) При создании нового узла необходимо «сносить» точку на поверхность f ( x , y , z )=0. Я использую для этого следующую итерацию:

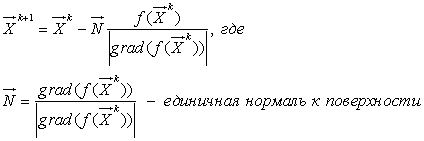
Это аналогично методу Ньютона для решения уравнения f(x)=0. Итерации прекращаются, когда шаг = f(Xk) / | grad ( f ( Xk ))| становится меньше заданной точности 0,005∆x.

III ) Угол между отрезками на границе следует определять с учетом кривизны поверхности – по касательным (проекциям отрезков на плоскость, касательную к поверхности) в точке.

IV ) Выпуклость тоже следует определять с учетом кривизны поверхности, по проекциям на касательную плоскость.

V ) Необходимо учесть, что возможны особые точки (в которых нормаль к поверхности не определена). Например, вершина оживальной оболочки (острый носик пули/снаряда). Процедура триангуляции может выйти за носик и начать создание сетки на воронке, являющейся поверхностью вращения продолжения огибающей. Чтобы гарантированно не промахнуться мимо этой особой точки, приходится вводить линию связности, состоящую из одной (особой) точки. Как только фронт достроения дойдет до носика, линии связности соединятся и граница пройдет через эту точку. Это влечет за собой еще одну особенность, которую необходимо предусмотреть – возможность существования линии связности, состоящую из одной точки, для которой уже не применимы понятия угла, длины отрезка и т.д.

Назад, на численное моделирование